深入浅出Factorization Machines系列
近期使用
FM系列完成了一个CTR预估的任务,本文是阅读了一些paper之后对于FM、FFM、DeepFM、NFM,AFM的一个理解和记录
FM
Factorization Machine(FM)由Steffen Rendle在2010年提出,旨在解决系数数据下的特征组合的问题,目前该系列模型在搜索推荐领域被广泛使用。
一个栗子
先来看一个经典的电影评分问题
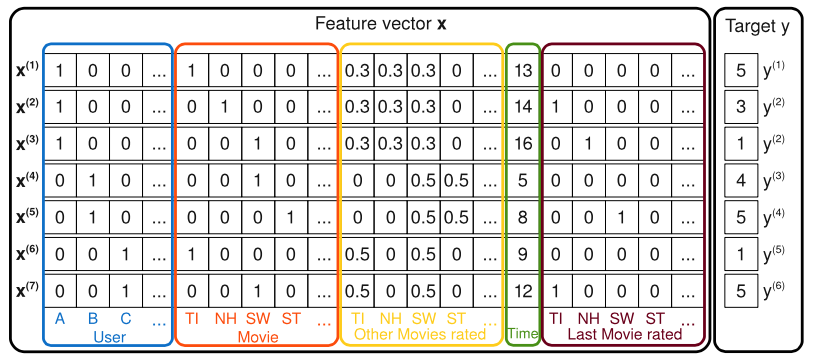
问题就是需要对电影进行评分($y$项),而$x$都是特征,其中:
- 第一部分蓝色的为当前评分的用户
- 第二部分红色的为被评分的电影
- 第三部分黄色的为该用户曾经对其他电影的评分情况
- 第四部分绿色的为该用户当前评分的月数
- 第五部分棕色为该用户最新一次评分的电影
这是一个经典的回归问题,最简单粗暴的方法就先上一个线性回归,其中对于绿色特征处理成binary,这样计算公式就是为
$$y_{lr} = w_0 + \sum_i^n w_i \cdot x_i$$
这样可能会过于简单粗暴,按照算法(特征)工程师的套路会对某些特征进行组合,这样为了方便,咱们就给他来一个全组合:
$$y_{lr-cross} = w_0 + \sum_i^n w_i \cdot x_i + \sum_i^n \sum_{j=i+1}^n w_{i,j} x_i x_j$$
看似问题解决了,但是这样会存在这么几个问题:
- 参数空间过大,这里为$O(n^2)$,在处理互联网数据时,特征两级别可能是亿级别的
- 需要人工经验,这里一般会选择某些特征来组合,此时人工/专家经验就会很重要
- 样本量过滤稀疏,实际上那这种方式拿到的特征会是很稀疏的,对于在训练样本中未出现过的组合该模型无能为力
FM解法
定理:对于一个正定举证$W$,始终存在一个矩阵$V$使得$W=V \cdot V^t$成立(需要$V$的维数$k$足够大)
但是在巨大稀疏矩阵的情况下,当$k$并不是很大时$V \cdot V^t$也可以很接近$W$,因此可以用
$$w_{i,j} = \left \langle v_i,v_j \right \rangle = \sum_f^k v_{i,f} \cdot v_{j,f}$$
其中这里$v$为长度$k$的一个向量,$\left \langle v_i,v_j \right \rangle$表示两个向量的点积,在FM中也称为隐向量,这样就有了FM的式子:
$$y := w_0 + \sum_i^n w_i \cdot x_i + \sum_{i=1}^n \sum_{j=i+1}^n \left \langle v_i,v_j \right \rangle x_i x_j$$
到了这里FM的式子:
- 可以解决稀疏向量问题,因为每个特征都有一个隐向量,就算是稀疏向量在训练样本没有出现过的组合在预测时也可以进行计算
- 同时参数空间也降低到了$O(n\cdot k)$
但是他实际的运算复杂度并没有降低,反而还到了$O(kn^2)$,但是FM这里的二阶项并没有依赖其他模型参数除了$v_i$,这里就可以鬼斧神工的写为:
$$\begin{equation}\begin{split} \sum_{i=1}^n \sum_{j=i+1}^n \left \langle v_i,v_j \right \rangle x_i x_j &= \frac{1}{2}\sum_{i=1}^n \sum_{j=1}^n \left \langle v_i,v_j \right \rangle x_i x_j - \frac{1}{2} \sum_{i=1}^n \left \langle v_i,v_i \right \rangle x_i x_i \\
&= \frac{1}{2} \left ( \sum_{i=1}^n \sum_{j=1}^n \sum_{f=1}^k v_{i,f} v_{j,f} x_i x_j - \sum_{i=1}^n \sum_{f=1}^k v_{i,f} v_{i,f} x_i x_i \right ) \\
&= \frac{1}{2} \sum_{f=1}^k \left[ \left ( \sum_{i=1}^n v_{i,f}x_i \right ) \left( \sum_{j=1}^n v_{j,f}x_j \right ) -\sum_{i=1}^n v_{i,f}^2 x_i^2 \right ] \\
&= \frac{1}{2} \sum_{f=1}^k \left[ \left ( \sum_{i=1}^n v_{i,f}x_i \right )^2 -\sum_{i=1}^n v_{i,f}^2 x_i^2 \right ]
\end{split}\end{equation}$$
经过这样的转换之后,最终的模型计算复杂度将会降低到$O(kn)$,同时由于是巨大的稀疏场景,样本实际的特征量的平均值为$\bar{m}$并且$\bar{m}<<n$,最终的模型复杂度将会降低到$O(k \bar{m})$
FM学习
在FM中模型的参数有$w_0$,$W$以及$V$,这些参数可以通过梯度下降法进行高效的计算,其中梯度为:
$$ \frac{\partial}{\partial \theta}y(x)=\left\{
\begin{aligned}
1 & \quad if \quad \theta = w_0 \\
x_i & \quad if \quad \theta = w_i \\
x_i \sum_{j=1}^n v_{j,f}x_j-v_{i,f}x_i^2 & \quad if \quad \theta = v_{i,f} \\
\end{aligned}
\right.$$
其中$\sum_{j=1}^n v_{j,f}x_j$部分与$i$相互独立,可以预先计算出来,另外
FM在过拟合方面一般推荐使用L2正则项
所以在梯度计算方面可以在$O(1)$下进行计算
作者也提供了一个很强大的开源工具来训练FM:http://www.libfm.org
扩展
其实对于经典的特征组合问题,也非常容易能想到使用万能的SVM来求解,比如一个二阶的多项式SVM可以写成这样:
$$y_{svm} = w_0 + \sqrt{2} \sum_{i=1}^n w_ix_i + \sum_{i=1}^n w_i^{(2)}x_i^2 + \sqrt{2} \sum_{i=1}^n \sum_{j=i+1}^n w_{i,j}^{(2)}x_ix_j$$
这样可以发现二阶多项式的svm和FM十分相似,只多了一项$\sum_{i=1}^n w_i^{(2)}x_i^2$,但是SVM对于未出现在训练样本的组合特征也是无法计算,同时他需要使用对偶才能进行求解,并且他在预测的时候还需要训练样本的支持向量。
另外FM还可以用于tag的推荐排序,问题描述是给定用户信息$U$,宝贝信息$I$,对于相应的标签T进行排序,在binary特征下面模型可以表述为:
$$n:= |U \cup I \cup T|, \quad x_i=\delta (j=i \vee j=u \vee j=t)$$
使用FM的计算为
$$y(x) = w_0 +w_u+w_i+w_t+\left \langle v_u,v_i \right \rangle + \left \langle v_u,v_t \right \rangle + \left \langle v_i,v_t \right \rangle $$
但是在排序问题上,当对于tagA,tagB进行排序时,他们的$w_0 +w_u+w_i+\left \langle v_u,v_i \right \rangle$分项计算其实是一样的,所以FM模型最终在tag排序的问题上可以简化为:
$$y(x):=w_t+ \left \langle v_u,v_t \right \rangle + \left \langle v_i,v_t \right \rangle$$
这样就是PITF模型极为相似了.
当然上面说的都是二阶FM,其实FM还是支持多阶的,只是由于性能/效率问题一般二阶就够了,感兴趣的同学可以去看原始paper
FFM
FFM其实是在FM的基础上做了一些更加细致化的工作:作者Yuchin认为相同性质的特征归于同一field,而当前特征在不同field上的表现应该是不同的.
比如在广告领域中性别对于广告商(Advertiser)和投放地(Publisher)的作用就是不一样的,比如:
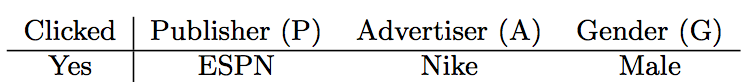
这里的特征被分为了三类,有投放地(Publisher),广告商(Advertiser)和性别(Gender),如果使用FM来预估这个点击率则是:
$$\left \langle v_{ESPN},v_{Nike} \right \rangle + \left \langle v_{ESPN},v_{Male} \right \rangle + \left \langle v_{Nike},v_{Male} \right \rangle$$
这里可以看出FM中隐向量对于不同类别的特征进行组合时都是使用同一个向量,而基于Field-aware的FFM就是对这点进行修改,认为当前向量对于每一个类别都有一个不同的隐向量,比如性别和投放地进行组合的时候使用的隐向量为$v_{Male,G}$,这样推广开来之后这个问题中FFM的二阶项就可以表述为:
$$ \left \langle v_{ESPN,A},v_{Nike,P} \right \rangle + \left \langle v_{ESPN,G},v_{Male,P} \right \rangle + \left \langle v_{Nike,G},v_{Male,A} \right \rangle$$
这样,FFM使用通用化的学习公式表达了之后为:
$$y_{FFM}(x) = w_0 + \sum_i^n w_i \cdot x_i + \sum_{i=1}^n \sum_{j=i+1}^n \left \langle v_{i,f_j},v_{j,f_i} \right \rangle x_ix_j$$
因为FFM的参数空间为$nfk$,其计算复杂度为$O(\bar{n}k)$,但是FFM都是在特定的field的中来学习训练隐向量的,所以一般来说:
$$k_{FFM} << k_{FM}$$
其实我实际试用下来这里的$<<$不是很严谨,
FM的$k$也并没有比FFM多太多,也许只可能是一个8和4的差别。-_-!!
FFM的改进看上去还是有挺有道理的,但是其实最终实验做出来和FM的效果不相上下:
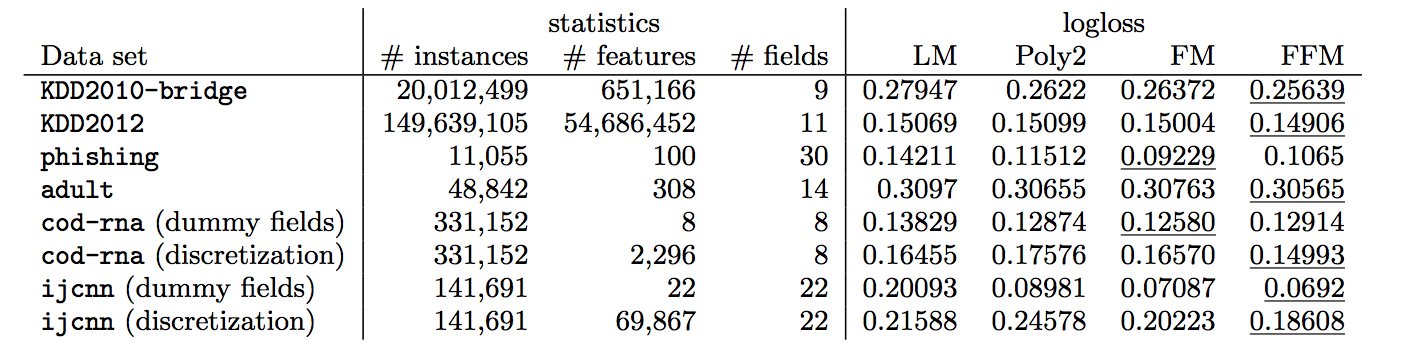
实验结果上FFM也只是在某几个数据集上略好于FM,但是由于FFM中的隐向量与field有关,无法直接转为FM中的$O(k\bar{n})$的运算式子,所以在工业界追求运行效率的时候FM还是首选,不过是比赛中FFM也是一个不错的选择.
这里符一下
FFM的开源工具代码:https://www.csie.ntu.edu.tw/~cjlin/libffm/,注意里面有有提供只含二阶项的版本和同时含线性计算的版本.
DeepFM
受到Wide&Deep的启发,Huifeng等人将FM和Deep深度学习结合了起来,简单的说就是将Wide部分使用FM来代替,同时FM的隐向量可以充当Feature的Embedding,非常巧妙:
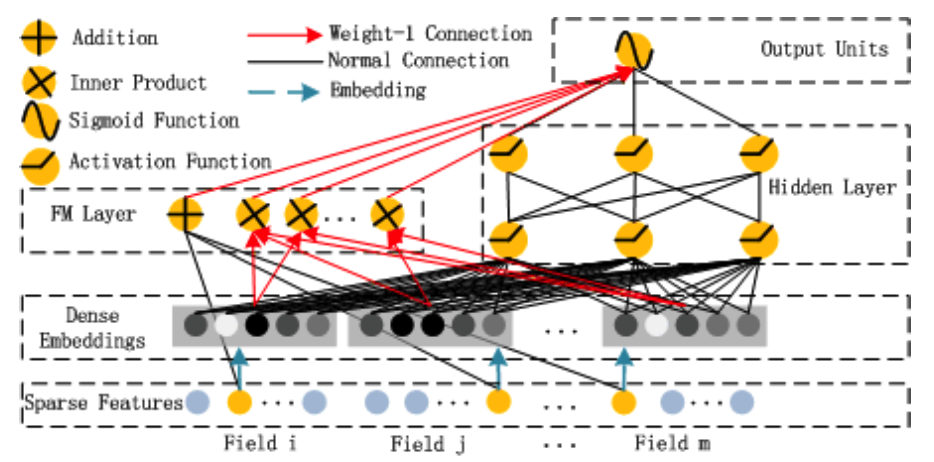
DeepFM的架构其实特别清晰:
- 输入的是稀疏特征的id
- 进行一层lookup 之后得到id的稠密embedding
- 这个embedding一方面作为隐向量输入到FM层进行计算
- 同时该embedding进行聚合之后输入到一个DNN模型(deep)
- 然后将FM层和DNN层的输入求和之后进行co-train
因为最终计算的式子也是非常清晰的明了:
Fm部分:
$$y_{\text{FM}} = \left \langle W,X \right \rangle + \sum_i^n \sum_{j=i+1}^n \left \langle v_i,v_j \right \rangle x_i x_j$$
Deep部分:
$$a(0) =[e ,e ,…,e ] \\
a(l+1) = \sigma (W^{(l)}a^{(l)} + b^{(l)}) \\
y_{\text{DNN}} = \sigma (W^{(H+1)}a^{H} + b^{(H+1)})$$
其中$e$表示初始的embedding,$H$表示网络的深度
最终DeepFM可以表示为:
$$y_{\text{DeepFm}} = sigmoid(y_{FM} + y_{DNN})$$
这个结合非常有意思,充分将FM中隐向量含element-wise product的功能结合到了DNN中,公司有实测DeepFM的效果略好于的Wide&Deep,因此该算法还是非常有实操性的,特别是在公司里面要出成(zhuang)果(bi)的时候。
DeepFm的非作者源码分享https://github.com/ChenglongChen/tensorflow-DeepFM
NFM
NFM(Neural Factorization Machines)又是在FM上的一个改进工作,出发点是FM通过隐向量可以对完成一个很好的特征组合工作,并且还解决了稀疏的问题,但是FM对于它对于non-linear和higher-order 特征交叉能力不足,而NFM则是结合了FM和NN来弥补这个不足。模型框架如下(图里没画一阶的回归):
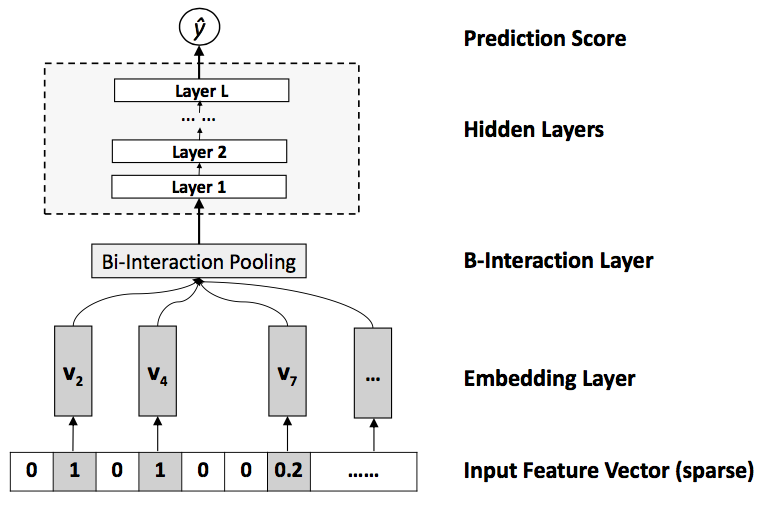
其中:
1.
Input Feature Vector层是输入的稀疏向量,可以带权2.
Embedding Layer对输入的稀疏向量look up 成稠密的embedding 向量3.
Bi-Interaction Layer将每个特征embedding进行两两做element-wise product,Bi-Interaction的输出是一个 k维向量(就是隐向量的大小),这层负责了特征之间second-order组合。$$f_{\text{Bi}}(V_x) = \sum_i^n \sum_{j=i+1}^n x_iv_i \odot x_jv_j$$ 类似FM的式子转换,这里同样可以做如下转换将复杂度降低:$$f_{\text{Bi}}(V_x) = \frac{1}{2} \left [ (\sum_i^n x_iv_i)^2 - \sum_i^n(x_iv_i)^2 \right ]$$4.
Hidden Layers这里是多层学习高阶组合特征学习,其实就是一个DNN模块:$$z_1=\sigma_1(W_1 f_{\text{Bi}}(V_x) + b_1) \\ z_2 = \sigma_2(W_2z_1+b_2) \\ … \\ z_L=\sigma_L(W_L z_{L-1}+b_L)$$5.
Prediction Score层就是输出最终的结果:$$y_{\text{NFM}}(x) = w_0 + \sum_i^n w_ix_i + h^T \sigma_L(W_l(…\sigma_1(W_1 f_{\text{Bi}}(V_x) + b_1))+b_L)$$FM可以看做是NFM模型 Hidden Layer层数为0一种特殊形式。
最终的实验效果看来
NFM也还是可以带来一个不错的效果: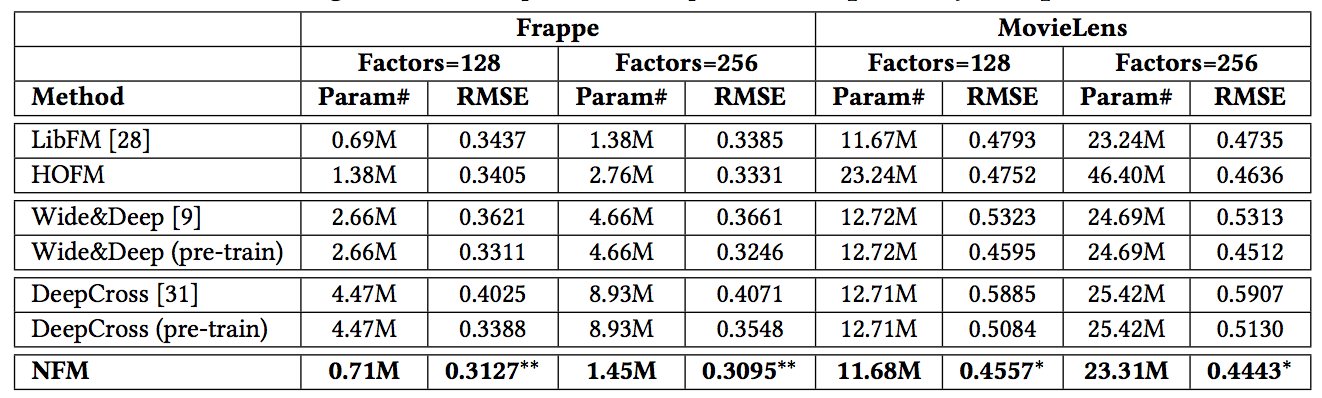
NFM作者分享的源码https://github.com/hexiangnan/neural_factorization_machine
AFM
而AFM(Attentional Factorization Machines)同样,是在FM上做了一些小trick,在传统的FM中进行特征组合时两两特征之间的组合都是等价的(只能通过隐向量的点积来区别),这里趁着Attention的热度走一波,因为AFM的最大的贡献就是通过Attention建立权重矩阵来学习两两向量组合时不同的权重。下面就是AFM的框架图:
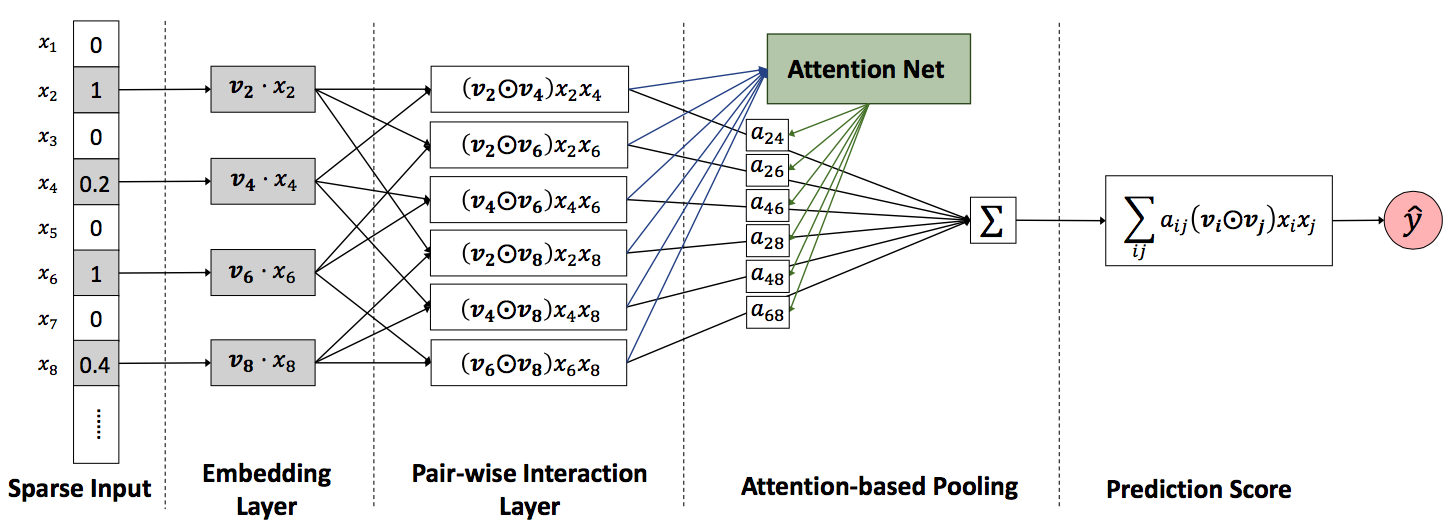
从图中可以很清晰的看出,
AFM比FM就是多了一层Attention-based Pooling,该层的作用是通过Attention机制生成一个$a_{i,j}$权重矩阵,该权重矩阵将会作用到最后的二阶项中,因此这里$a_{i,j}$的生成步骤是先通过原始的二阶点积求得各自的组合的一个score:$${a}’_{i,j} = h^T \text{ReLu}(W(v_i \odot v_j)x_ix_j+b)$$
> 其中$W \in \mathbb{R}^{t \times k},b \in \mathbb{R}^t , h \in \mathbb{R}^t$,这里$t$表示
Attention网络的大小然后对其score进行
softmax的归一化:$$a_{i,j} = \frac{exp({a}’_{i,j})}{\sum_{i,j} exp({a}’_{i,j})}$$
最后该权重矩阵再次用于二阶项的计算(也就是最终的
AFM式子):$$y_{\text{AFM}}(x) = w_0+\sum_i^n w_i x_i + P^T \sum_{i=1}^n \sum_{j=i+1}^n a_{i,j} (v_i \odot v_j) x_ix_j$$
其实整个算法思路也是很简单,但是在实验上却有一个不错的效果:
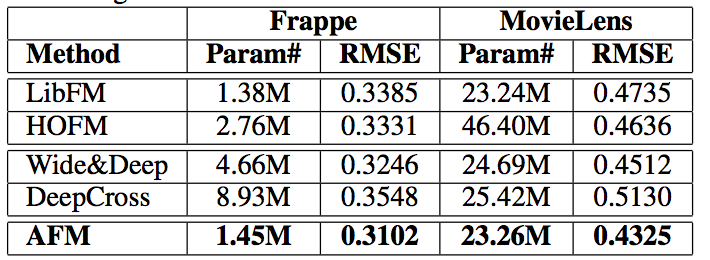
其实从实验效果来看
AFM应该是优于NFMAFM的作者源码分享https://github.com/hexiangnan/attentional_factorization_machine
总结
FMs系列算法被广泛应用于ctr预估类的问题中,并且可以取得不错的效果,他最大特征是可以帮助解决特征组合问题- 原始
FM算法的运行性能最快,可以达到$O(k \bar{n})$,在工业中被适用最广最简单,其他带上神经网络的FM算法如果想在在线系统中使用得做很多离线计算和分解,比如FFM的现在复杂度是$O(k \bar{n}^2)$,将$O(\bar{n}^2)$中二阶计算的项尽可能的进行离线计算,在 在线的时候进行组合 FM的二阶项部分很容易使用TensorFlow进行实现,这也意味了在实验上也很容易很其他复杂算法进行组合:
1 | # get the summed up embeddings of features. |
摘自
AFM源码
参考
[1]. Rendle, Steffen. “Factorization machines with libfm.” ACM Transactions on Intelligent Systems and Technology (TIST) 3.3 (2012): 57.
[2]. Juan, Yuchin, et al. “Field-aware factorization machines for CTR prediction.” Proceedings of the 10th ACM Conference on Recommender Systems. ACM, 2016.
[3]. Guo, Huifeng, et al. “Deepfm: A factorization-machine based neural network for CTR prediction.” arXiv preprint arXiv:1703.04247 (2017).
[4]. He, Xiangnan, and Tat-Seng Chua. “Neural factorization machines for sparse predictive analytics.” Proceedings of the 40th International ACM SIGIR conference on Research and Development in Information Retrieval. ACM, 2017.
[5]. Xiao, Jun, et al. “Attentional factorization machines: Learning the weight of feature interactions via attention networks.” arXiv preprint arXiv:1708.04617 (2017).

